문제 주소 : www.acmicpc.net/problem/2315
2315번: 가로등 끄기
첫째 줄에는 2개의 정수 N(1 ≤ N ≤ 1,000), M 이 있다. 첫 번째 정수 N은 가로등의 개수를 나타내는 정수이고, 두 번째 정수 M은 마징가 처음에 위치하는 가로등 번호이다. 다음 N 개의 줄에는 각 가
www.acmicpc.net

문제 확인
dp 응용문제입니다.
지나치는 길의 가로등은 끄는 것이 이득이므로 지나친 지점의 가로등을 고려할 필요는 없습니다.
따라서 dp 스텝을 총 2가지로 분류할 수 있습니다.
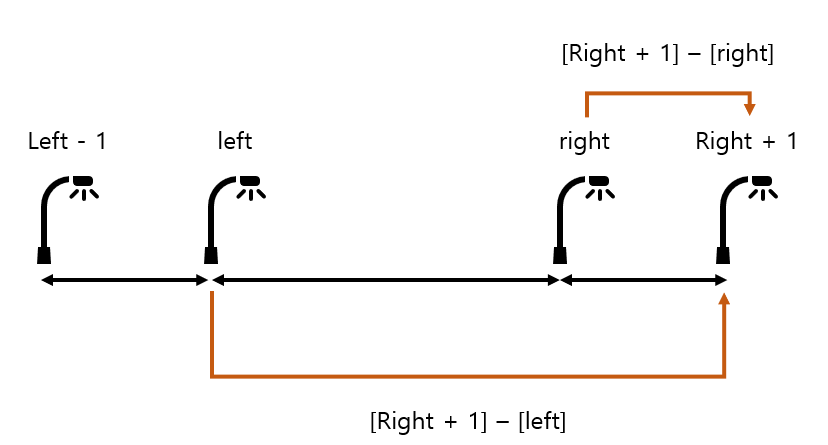
left : right 사이의 가로등을 모두 끈 상태에서 left : right + 1 상태로 전의 하는 방법 ==>
- left 에서 right + 1로 이동 : 이동거리 = ary[right + 1] - ary[left]
- right 에서 right + 1로 이동 : 이동거리 = ary[right + 1] - ary[right]
반대 방향의 경우도 같습니다. left : right --> left - 1 : right
- left 에서 left - 1로 이동 : 이동거리 = ary[left] - ary[left - 1]
- right 에서 left - 1로 이동 : 이동거리 = ary[right] - ary[left - 1]
가로등의 에너지 소비량을 prefix sum을 통해 미리 계산 해 두어 dp 시 계산량을 적게 만들어 줍니다.
이동하는 동안 소비하는 에너지는 left : right 사이에 있는 가로등을 제외한 나머지 가로등입니다.
= w[n] - (w[right] - w[left - 1])
풀이
스텝을 점화식으로 만들어 봅니다. 이때 고려해야 할 점은 left : right 상태에서 현재 위치가 left, right 중 어느 위치인지 구분을 할 필요가 있습니다. 이를 위하여 dp 배열을 dp[][][2]로 선언을 하여 구분을 합니다.
dp[left][right][tag]= min(
solve(left - 1, right, false) + consume * (tag ? ary[right] - ary[left - 1] : ary[left] - ary[left - 1]),
solve(left, right + 1, true) + consume * (tag ? ary[right + 1] - ary[right] : ary[right + 1] - ary[left]));
로 둘 수 있습니다. tag의 경우 현재 dp[left][right] 상태에서 left, right 중에서 어느 위치에 있는지를 알기 위한 변수입니다.

위와 같은 식으로 재귀 함수를 통해 바텀-업 방식으로 계산을 하면 조금 느린것을 볼 수 있습니다.
재귀함수를 사용하지 않고 이 문제를 풀어보겠습니다.
현재 위치가 left 인 경우
dp[left][right][0] = min(dp[left - 1][right][0] + consume * (ary[left] - ary[left - 1]),
dp[left][right + 1][1] + consume * (ary[right + 1] - ary[left]))
right 인 경우
dp[left][right][1] = min(dp[left - 1][right][0] + consume * (ary[right] - ary[left - 1]),
dp[left][right + 1][1] + consume * (ary[right + 1] - ary[right]))
결과 4ms로 줄일 수 있었습니다.
코드
재귀
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#include <cstdio>
#include <algorithm>
using namespace std;
int n, m, ary[1001], w[1001] = { 0 }, wt, dp[1001][1001][2];
int solve(int left, int right, bool tag) {
if (dp[left][right][tag])return dp[left][right][tag];
else if (left==1 && right==n) return dp[left][right][tag] = 0;
int val = 0x7fffffff, consume = wt - (w[right] - w[left - 1]);
if (left>1)
val = solve(left - 1, right, false) +
consume * (tag ? ary[right] - ary[left - 1] : ary[left] - ary[left - 1]);
if (right<n)
val = min(val, solve(left, right + 1, true) +
consume * (tag ? ary[right + 1] - ary[right] : ary[right + 1] - ary[left]));
return dp[left][right][tag] = val;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &ary[i], &w[i]);
w[i] += w[i - 1];
}
wt = w[n];
printf("%d", solve(m,m, false));
}
|
cs |
반복문
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
#include <cstdio>
#include <algorithm>
using namespace std;
int main() {
int n, m, ary[1001], w[1001] = { 0 }, wt, dp[1001][1001][2] = { 0 };
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &ary[i], &w[i]);
w[i] += w[i - 1];
}
wt = w[n];
int right = n - 1;
for (int left = 1; left <= m; ++left) {
for (; right >= m; --right) {
int x = 0x7fffffff, y = 0x7fffffff, consume = wt - (w[right] - w[left - 1]);
if (left != 1) {
x = min(x, dp[left - 1][right][0] + consume * (ary[left] - ary[left - 1]));
y = min(y, dp[left - 1][right][0] + consume * (ary[right] - ary[left - 1]));
}
if (right != n) {
x = min(x, dp[left][right + 1][1] + consume * (ary[right + 1] - ary[left]));
y = min(y, dp[left][right + 1][1] + consume * (ary[right + 1] - ary[right]));
}
dp[left][right][0] = x;
dp[left][right][1] = y;
}
right = n;
}
printf("%d", min(dp[m][m][0], dp[m][m][1]));
}
|
cs |
'알고리즘 문제 > [백준]' 카테고리의 다른 글
| [백준] 1867 돌멩이 제거 (0) | 2020.12.31 |
|---|---|
| [백준] 1208 부분수열의 합 2 (0) | 2020.12.29 |
| [백준] 1150 백업 (0) | 2020.12.19 |
| [백준] 8895 막대 배치 (0) | 2020.12.18 |
| [백준] 15685 드래곤 커브 (0) | 2020.12.17 |