[자료구조] 세그먼트 트리

자료구조 설명 : www.acmicpc.net/blog/view/9

세그먼트 트리 (Segment Tree)

백준 사이트에서 설명을 잘해 두었습니다.

배열에서 부분합, 부분 최대/최소 등 범위 참조 연산이 자주 일어날 때 자주 사용하는 자료구조입니다. 미리 배열에 대하여 세그먼트 트리를 생성해 둔 후 미리 계산해둔 값을 참고하여 O(n)의 시간을 O(log n) 만큼으로 줄여줍니다.

 

백준: 세그먼트 트리 구조

일반적으로 세그먼트 트리에서 노드들은 다음과 같은 의미를 가집니다.

1. 리프 노드 : 배열의 실제 데이터
2. 그 외 : 왼쪽 범위, 오른쪽 범위의 값들을 연산한 결과

따라서 필요한 범위가 0~7이면 0~4, 5~9 -> 5~7 = 총 3번의 접근만에 결과를 낼 수 있습니다.

 

백준 사이트 에서 트리 생성, query 과정이 모두 재귀 함수로 이루어져 있어 이를 dp를 활용하여 iterative 하게 만들어 봅니다. 이 결과 백준 사이트에서 사용하는 세그먼트 트리의 구조와 조금 다릅니다.

 

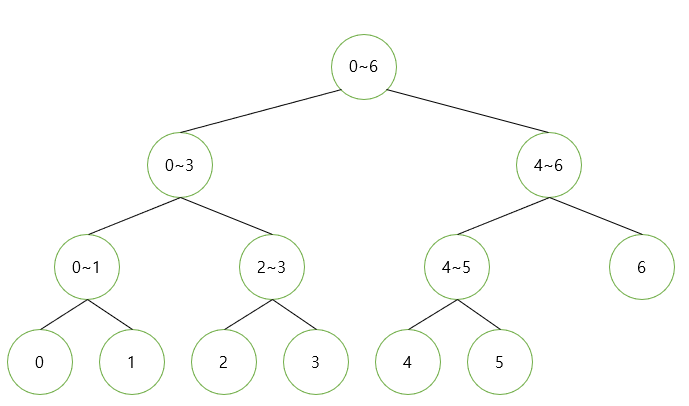
위와 같은 형식으로 초기 데이터에서 2개씩 짝을 지어 올라가는 형태로 dp와 유사한 과정을 거치게 됩니다. query 또한 마찬가지로 아래에서 위로 향하면서 연산합니다.

이때 2개씩 짝지은 특성에 의해 중간 노드들의 범위는 (짝수, 짝수 or 홀수) 형테로 되며 홀수인 경우에 한하여 연산을 통해 범위를 구해나가 연산 횟수를 줄일 수 있습니다.

 

코드

예시 문제 : www.acmicpc.net/problem/10868

10868번: 최솟값

 

#include <cstdio>
#include <algorithm>
using namespace std;
int main() {
    int tree[200002];
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i++)
        scanf("%d", &tree[n + i]);
    for (int i = n - 1; i > 0; i--)
        tree[i] = min(tree[i << 1], tree[i << 1 | 1]);
    while (m--) {
        int s, e, mn = 0x7fffffff;
        scanf("%d%d", &s, &e);
        for (s += n - 1, e += n; s < e; s >>= 1, e >>= 1) {
            if (s & 1) mn = min(tree[s++], mn);
            if (e & 1) mn = min(tree[--e], mn);
        }
        printf("%d\n", mn);
    }
}