Wiki : en.wikipedia.org/wiki/Binomial_heap
Binomial heap - Wikipedia
In computer science, a binomial heap is a data structure that acts as a priority queue but also allows pairs of heaps to be merged. It is important as an implementation of the mergeable heap abstract data type (also called meldable heap), which is a priori
en.wikipedia.org
Visualization : www.cs.usfca.edu/~galles/visualization/BinomialQueue.html
Binomial Queue Visualization
www.cs.usfca.edu
The binomial heap consists of a combined binomial tree and the binomial tree of n order consists of two n-1 order binomial trees. Wikipedia explains it in a slightly different way.
- The children of the root node of an n-order binomial tree are n-1, n-2, n-3... 2, 1 binomial tree.
The binomial tree of n order has a property of 2^n nodes.

binomial heap
The binomial heap consists of a set of this binomial tree.
Similar to the binary heap, the root node becomes a high weighted node, but it can have more than two child node.
The root nodes of the binomial tree are connected in a structure. There are several conditions for a binomial heap structure.
-
The root node of the binomial tree that comprises the binomial heap has the highest weight value in that binomial tree. = Each binomial tree follows a heap structure.
-
The binomial trees that make up the binomial heap can only have 0 or 1 tree per order.
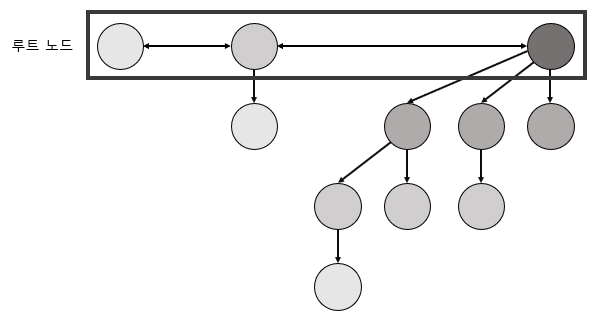
Merge
Before we do operations such as inserting or deleting from a heap, let's first look at merging trees, the basic operations that most operations use.
In the binomial tree, merge binomial trees of the same order to create an n+1 order binomial tree.
The first n order binomial tree described consists of two n-1 order binomial trees, which you can quickly understand.

Compare root nodes, set tree with high weighted node as root, and set low weight tree as child. Inserts the child nodes in front of them because the order of the child nodes in the merge is descending.
Because it simply compares and merges root nodes, it takes very little time. When inserted or deleted, it is implemented using the merge operation.
Insertion
Insert operation simply creates a new binary tree with zero order and merges it into the binomial heap.

If the heap does not have a zero order binary tree, new connections to the root node end the insertion.
As above, if the zero order node is in the heap, it is possible to have only zero or one tree per order of the binary heap conditions, resulting in the merging of the two binary trees, resulting in a one-order binary tree.

Repeat this process until the binomial heap conditions are met.

insertion result
If all order binary trees from 0 to n are in the heap, a total of n+1 merges will take as long as O (log n) due to the merge process.
Delete
Delete from heap means deleting the node with the highest weight.
For example, a deletion in the minimum binomial heap means the delete of minimum key node.
The process is a bit complicated, so I'll borrow Wikipedia's paintings.

Binary heap minimum deletion
a, b) Locate the root node's maximum value and detach the corresponding tree from the heap.
c) After deleting the root from the detached binomial tree, the children also have a binary heap structure. Merge these trees into an existing heap.
* In order to reduce the merge operation, I will delete the root and leave n - 1, n - 2 without merging in the order of least order as shown in the figure. We proceeded the merge in order of two and one. I used this method because I thought merging the tree of n order would create a tree of n+1 and merging the tree of n - 1 order would create a tree of n order, so merging the tree of the highest order first would result in a chain merger of only the tree of the highest order, and a single merger of the tree of the remaining order would be more efficient.
Code
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
|
#include <cstdio>
#include <queue>
using namespace std;
typedef struct node {
int key;
int degree;
node *down, *right;//child, sibling
node(int key) : key(key), degree(0), down(NULL), right(NULL) {};
}node;
node *binomial_heap;
void merge_tree(node *a, node* b) {//merge tree a <- b
node *prev = NULL;
for (; a && a->degree < b->degree; prev = a, a = a->right);
if (!a) {
prev->right = b;
b->right = NULL;
}
else if (a->degree != b->degree) {//insert middle or end
if (prev)
prev->right = b;
b->right = a;
}
else {//merge
b->right = a->right;
while (b && a->degree == b->degree) {//Until a different order of node comes out
if (a->key > b->key) {//b => top
if (prev)
prev->right = b;
else//front node
binomial_heap = b;
b->degree++;
a->right = b->down;
b->down = a;
a = b;
b = b->right;
}
else {//a => top
a->degree++;
a->right = b->right;
b->right = a->down;
a->down = b;
b = a->right;
}//insert node at front of children
}
}
}
void insert(int key){
node *tmp_node = new node(key);
if (!binomial_heap || binomial_heap->degree) {//empty root or doesn't have 0 degree
tmp_node->right = binomial_heap;
binomial_heap = tmp_node;
}
else {//merge in order starting with a binomial tree with zero degree
merge_tree(binomial_heap, tmp_node);
}
}
void pop() {
if (!binomial_heap) {
printf("heap is empty\n");
return;
}
node *cur = binomial_heap, *min = binomial_heap, *prev = NULL, *min_prev = NULL;
while (cur) {//find min root
if (min->key > cur->key) {
min = cur;
min_prev = prev;
}
prev = cur;
cur = cur->right;
}
if (min_prev)
min_prev->right = min->right;
else//front node
binomial_heap = min->right;
cur = min->down;
delete min;//delete root
while (cur) {//merge heap and children
prev = cur;
cur = cur->right;
if (!binomial_heap || binomial_heap->degree) {//empty root or doesn't have 0 degree
prev->right = binomial_heap;
binomial_heap = prev;
}
else {//merge in order starting with a binomial tree with zero degree
merge_tree(binomial_heap, prev);
}
}
}
void print() {//level order
node* cur = binomial_heap;
queue<node*> que;
while (cur) {
printf("degree %d :\n%d\n", cur->degree, cur->key);
que.push(cur->down);
while (!que.empty()) {
node* tmp = que.front();
que.pop();
while (tmp) {
printf("%d ", tmp->key);
que.push(tmp->down);
tmp = tmp->right;
}
}
printf("\n");
cur = cur->right;
}
}
int main() {
int t;
while (1) {
printf("1: insert\n2: pop(min)\n3: print level order\n4: exit\noperation : ");
scanf("%d", &t);
switch (t) {
case 1:
printf("key : ");
scanf("%d", &t);
insert(t);
break;
case 2:
pop();
break;
case 3:
print();
break;
case 4:
return 1;
}
putc('\n', stdout);
}
}
|
cs |