17822번: 원판 돌리기
반지름이 1, 2, ..., N인 원판이 크기가 작아지는 순으로 바닥에 놓여있고, 원판의 중심은 모두 같다. 원판의 반지름이 i이면, 그 원판을 i번째 원판이라고 한다. 각각의 원판에는 M개의 정수가 적혀
www.acmicpc.net

문제 확인
구현 문제입니다.
풀이
후에 사용할 평균값을 빠르게 구할 수 있도록 모든 원소의 총합 total, 모든 원소의 개수 cnt를 미리 구해둡니다.
밴치마크를 기록해두고 이를 이용하여 회전 시 모든 배열의 원소를 수정할 필요 없도록 합니다.
밴치마크를 처음 0번째 원소가 있는 위치 즉 북쪽 위치의 원소를 가리키는 인덱스로 둡니다.
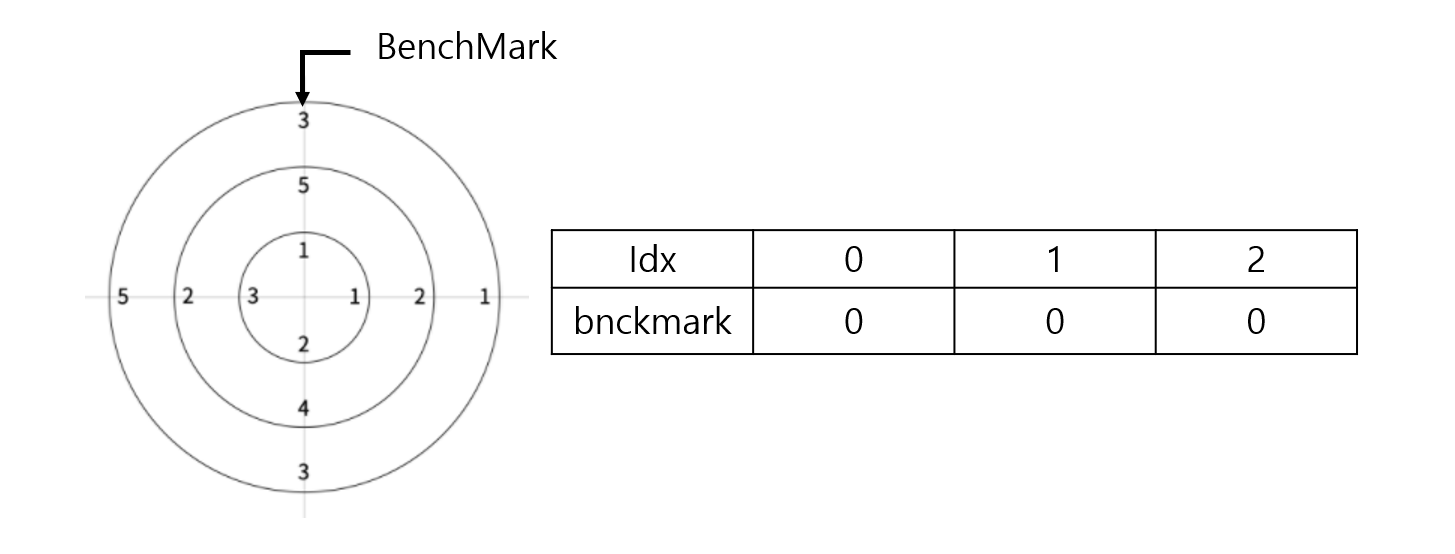
회전을 하게 되면 밴치마크가 가리키는 인덱스가 변하게 되며 회전 방향의 반대 방향의 인덱스가 설정됩니다.
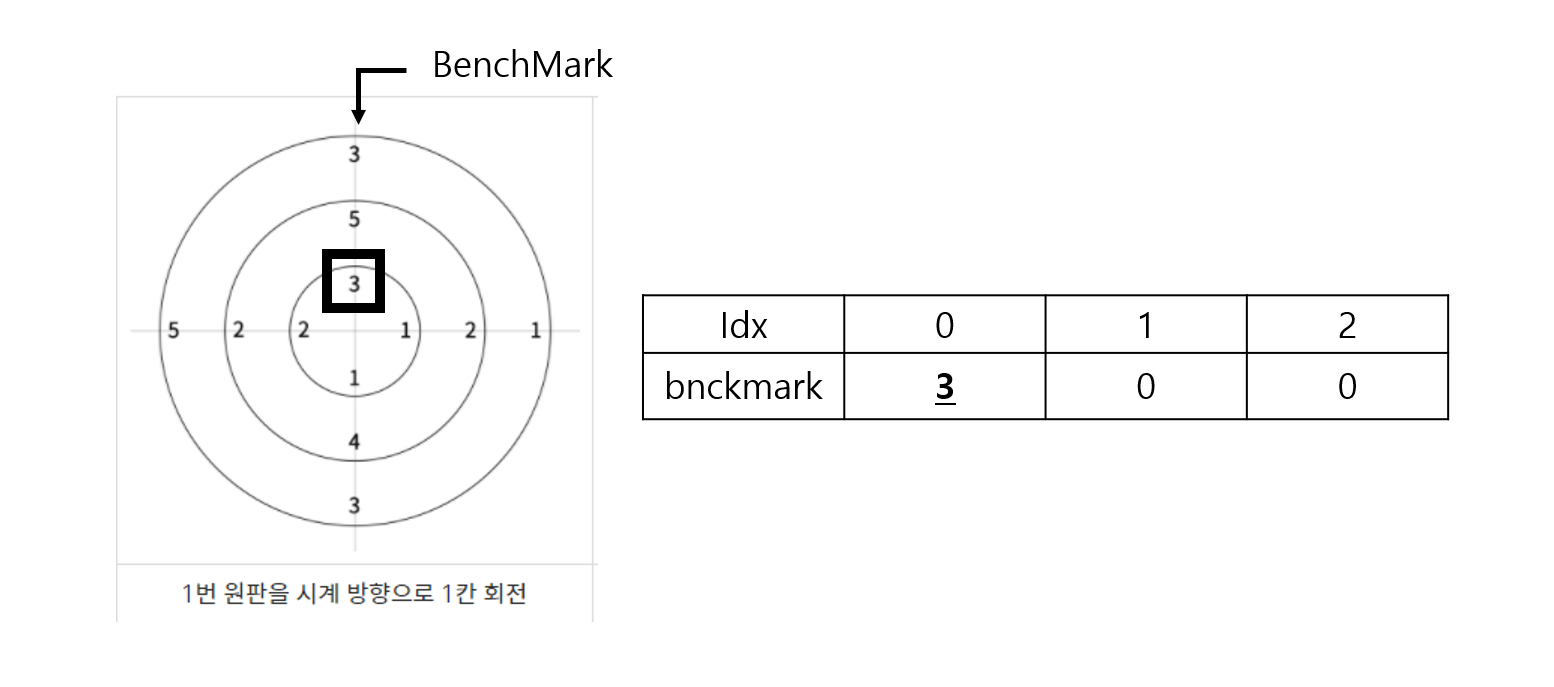
위와 같이 1번 원판을 시계방향으로 회전하면 밴치마크가 가리켜야 할 값은 3이 되고 이는 인덱스 [3]에 저장되어 있으므로 첫 번째 원판의 밴치마크 값은 3이 됩니다.
따라서 회전방향에 따라 다음과 같이 밴치마크를 수정합니다.
- 시계방향 d = 0 : bnchmark[i] = (bnchmark[i] + 회전 횟수) % m
- 반시계 방향 d = 1 : bnchmark[i] = (bnchmark[i] + 회전 횟수 + m) % m
다음으로 인접한 숫자가 같은 경우 이들을 제거해야 하는데 이때 검사할 값은 ary[i][(bnchmark[i] + j) % m] 이 됩니다.
이는 삼항 연산자 (bnchmark[i]+ j < m ? bnchmark[i] + j : bnchmark[i] + j - m)로 나타낼 수 있으므로 이를 사용합니다.
모듈러 연산보다 조건식 연산이 훨씬 빠르므로 이를 이용하는 것이 좋습니다.
모듈러, 삼항 연산자 성능 비교
Is it better to avoid using the mod operator when possible?
I assume that calculating the modulus of a number is a somewhat expensive operation, at least compared to simple arithmetic tests (such as seeing if a number exceeds the length of an array). If thi...
stackoverflow.com
인접 수가 같은 것을 탐색할 때 그래프 탐색을 이용하여도 좋지만 간단하게 2중 루프로 구현할 수 있습니다.
현재 수 ary[i][(bnchmark[i] + j) % m]가 인접한 수와 같은 경우 visited를 체크 해 두고 2중 루프가 끝나면 visited가 체크되어 있는 수 들을 모두 지워주면 됩니다.
인접수 :
ary[i][clockwise(idx, m)] : 시계방향에 위치한 수
ary[i][conterwise(idx, m)] : 반시계방향에 위치한 수
ary[i - 1][find_idx(bnchmark[i - 1], j)] : 현재 원판 바로 뒤의 큰 원판에 위치한 인접한 수
ary[i + 1][find_idx(bnchmark[i + 1], j)] : 현재 원판 앞에 작은 원판에 위치한 인접한 수
find_idx, clockwise, counterwise는 해당 위치의 원소를 찾기 위해 정의한 매크로입니다.
#define clockwise(idx, m) idx < m ? idx+1 : 1 : 시계방향의 좌표
#define counterwise(idx, m) idx > 1 ? idx-1 : m : 반시계 방향의 좌표
#define find_idx(bnck, j) (bnck + j < m ? bnck + j : bnck + j - m) + 1 : 밴치마크에서 j만큼 이동한 수
체크되어 있는 수 들을 지우면서 total과 cnt 값을 수정해 줍니다.
만약 인접한 수가 없어 지우지 않았다면 total과 cnt를 이용하여 평균 이상 인 수들은 -1, 평균 이하인 수 들은 +1 해주고 이 또한 total에 반영해줍니다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
#include<cstdio>
#define clockwise(idx, m) idx < m ? idx+1 : 1
#define counterwise(idx, m) idx > 1 ? idx-1 : m
#define find_idx(bnck, j) (bnck + j < m ? bnck + j : bnck + j - m) + 1
int main() {
int n, m, t;
scanf("%d %d %d", &n, &m, &t);
int ary[51][51], bnchmark[51] = { 0 };
int total = 0, cnt = m * n;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) {
scanf("%d", &ary[i][j]);
total += ary[i][j];
}
bool visited[51][51] = { 0 };
while (t--) {
int x, d, k;
scanf("%d %d %d", &x, &d, &k);
for (int i = x; i <= n; i += x) {
if (d)//반시계
bnchmark[i] = (bnchmark[i] + k) % m;
else//시계
bnchmark[i] = (bnchmark[i] + m - k) % m;
}
bool flag = 0;//수를 지워야 하는 경우의 수가 있음
for (int i = 1; i <= n; ++i)
for (int j = 0; j < m; ++j) {
int idx = find_idx(bnchmark[i], j);
if (ary[i][idx] && (ary[i][idx] == ary[i][clockwise(idx, m)] //시계방향 인접한 수
|| ary[i][idx] == ary[i][counterwise(idx, m)] ||//반시계방향
(i > 1 && ary[i][idx] == ary[i - 1][find_idx(bnchmark[i - 1], j)]) ||//큰 원판 인접한 수
(i < n && ary[i][idx] == ary[i + 1][find_idx(bnchmark[i + 1], j)]))) {//작은 원판
visited[i][idx] = 1;//지워야 할 수 체크
flag = 1;
}
}
if (flag) //지울 수가 있음
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) {
if (visited[i][j]) {
total -= ary[i][j];//수를 지우면 total, cnt 반영
cnt--;
ary[i][j] = 0;
visited[i][j] = 0;
}
}
else {//지운 수가 없음
if (cnt == 0) break;//더이상 수가 없으면 빠르게 종료
double avg = (double)total / cnt;//평균
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) {
if (!ary[i][j]) continue;
if (ary[i][j] < avg) {//평균이하
ary[i][j]++;
total++;
}
else if(ary[i][j]!=avg){//이상
ary[i][j]--;
total--;
}
}
}
}
printf("%d", total);
}
|
cs |
'알고리즘 문제 > [백준]' 카테고리의 다른 글
| [백준] 14890 경사로 (0) | 2021.04.08 |
|---|---|
| [백준] 1007 벡터 매칭 (0) | 2021.04.08 |
| [백준] 16719 ZOAC (0) | 2021.03.30 |
| [백준] 19237 어른 상어 (0) | 2021.03.28 |
| [백준] 9370 미확인 도착지 (0) | 2021.03.16 |